Understanding of fracture behavior is useful in selecting materials for product designs, and it is incredibly valuable to know if a material will experience a ductile-brittle transition and what temperature this transition occurs. Knowledge of a material's ductile-brittle transition temperature can prevent catastrophes such as the WW2 Liberty Ship failure.
Ductile fracture is characterized by a large amount of plastic deformation which leads to slow fracture that is often detectable before the material reaches a critical point. Conversely, brittle fracture contains very little plastic deformation and often little warning before fracture occurs.
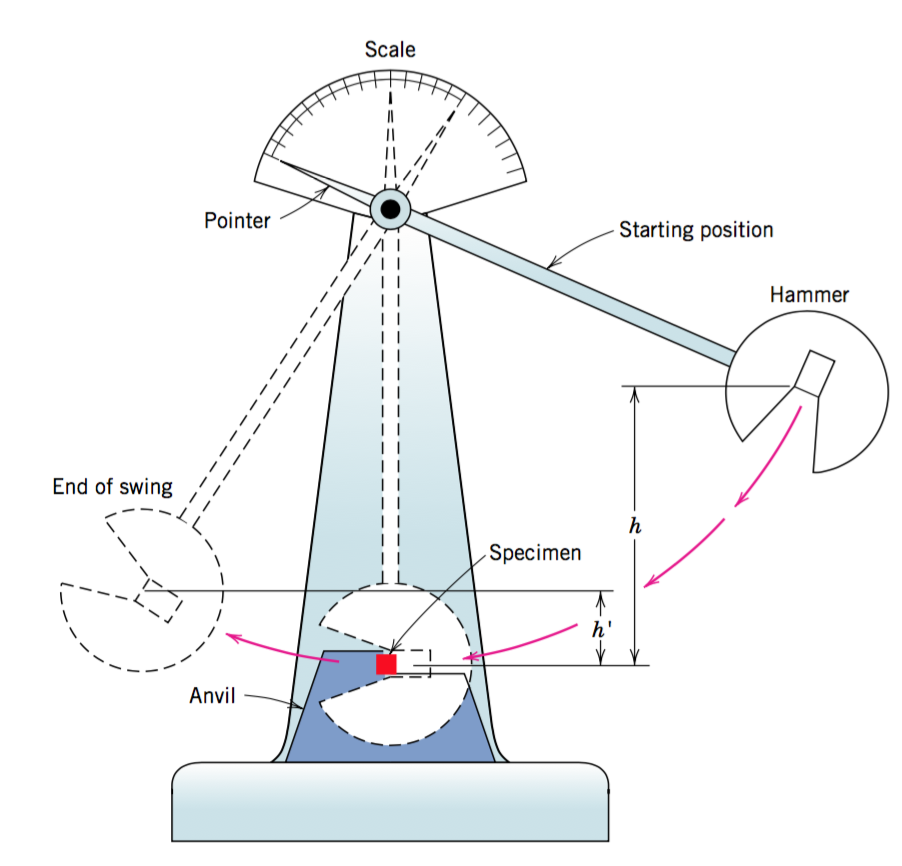
The Charpy impact test, depicted below, measures the amount of energy absorbed upon impact. A weighted pendulum, which is held at some height $h$ from the sample, swings and impacts the sample at a very high strain rate. The pendulum then continues to swing until reaching a final height of $h'$. The difference between the potential energies at height $h$ and $h'$ is considering to be the energy that the sample absorbed upon impact.
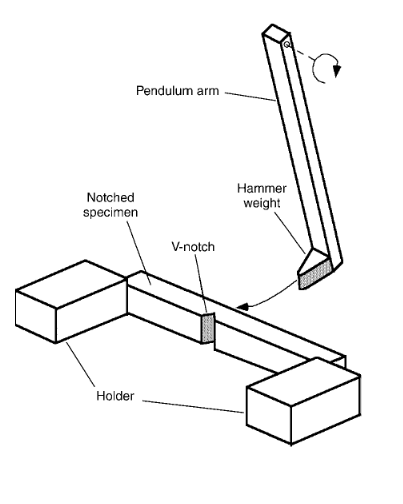
The sample for a Charpy impact test is notched to in order to control crack propagation and ensure consistent results across samples. The photo below displays a generic Charpy sample- note the V-shaped notch in the middle of the sample.
Fracture mechanics in materials ultimately extends to ease of dislocation movement. For samples in which dislocation motion in uninhibited, the material may accommodate an applied load through plastic deformation. For FCC metals, slip systems allow dislocations to move very easily along the close-packed planes. However, for BCC metals, there are no close-packed planes that allow for easy dislocation migration, and thus dislocation movement in these materials (BCC metals) require a thermal activation in order to slip. Otherwise, the material accommodates the applied stress through more drastic mechanisms, such as breaking of bonds.
An FCC unit cell with the close-packed plane shown in red.
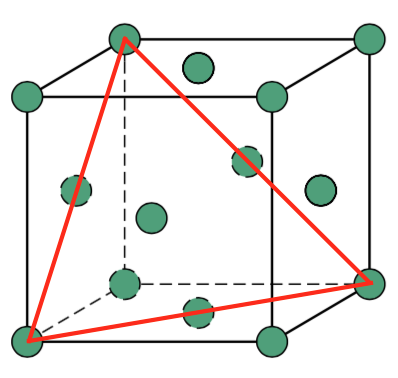
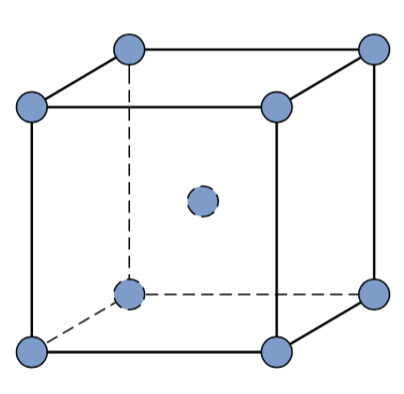
A BCC unit cell with no true close-packed plane. These psuedo-"slip" systems need some degree of thermal activation before they will operate.
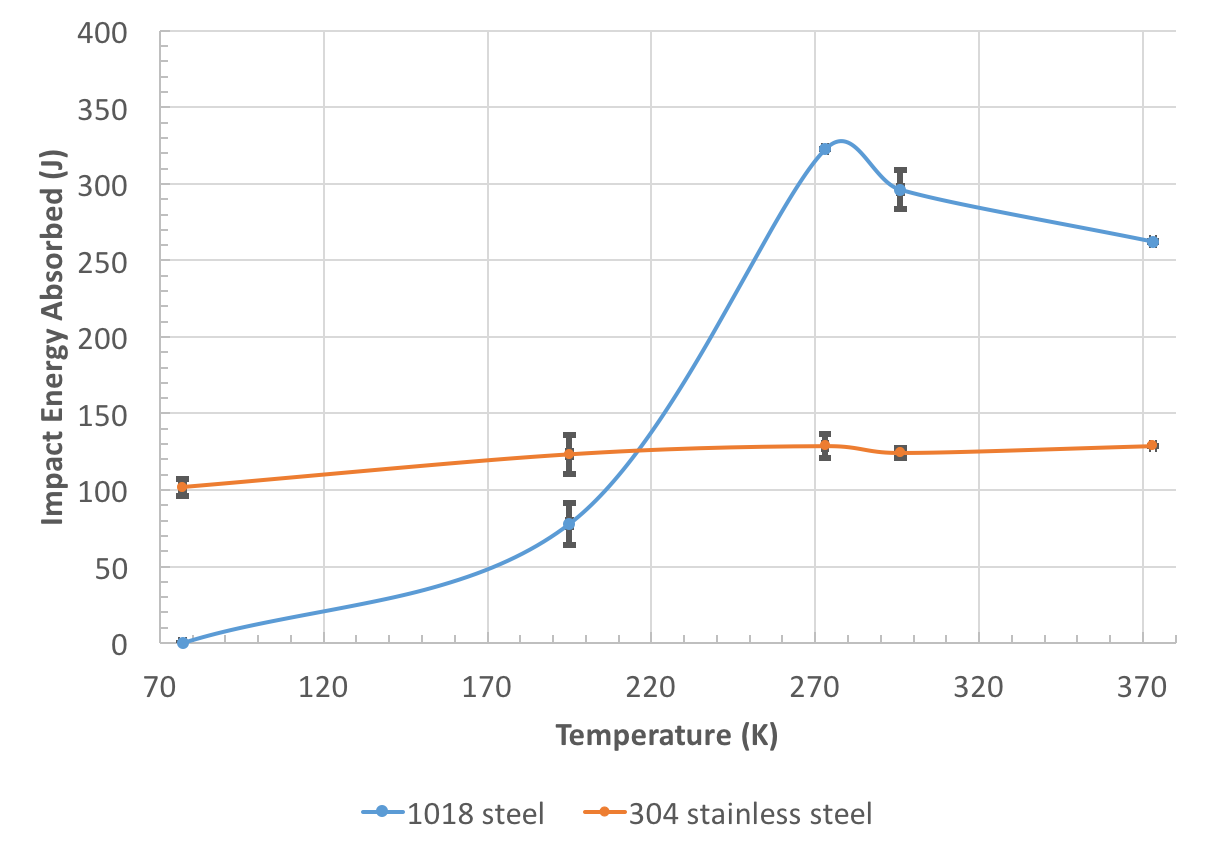
The figure below displays the general behaviors for various materials including FCC metals, BCC metals, and high-strength materials with regard to the Charpy impact test. A ductile-brittle transition temperature is observed for metals with a body-centered cubic structure as a result of the dependence on temperature for dislocation motion.
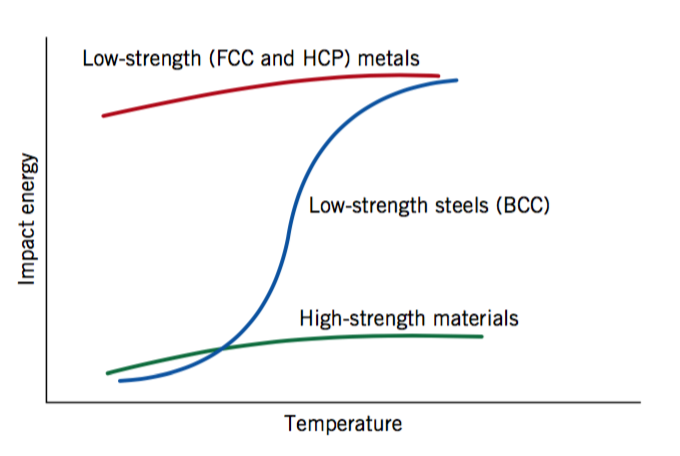
I'll provide some data from an undergrad lab experiment which examines the impact behavior for annealed 1018 steel and 304 stainless steel. Annealed 1018 steel is a low-strength BCC steel, which exhibits a ductile-brittle transition as shown above in the general behavior schematic. 304 stainless steel is a low-strength FCC metal, which has close-packed planes that allow for dislocation movement at all temperatures. Thus, this metal does not exhibit a ductile-brittle transition. The ductile-brittle transition temperature, $DBTT$, may be approximated as the temperature that corresponds with the energy calculated from
$DBTT = LSE + \frac{{USE - LSE}}{2}$
where $USE$ and $LSE$ represent the upper and lower shelf energies respectively. Generally, it reflects the inflection point on the logistic-type curves.