Activation functions are used to determine the firing of neurons in a neural network. Given a linear combination of inputs and weights from the previous layer, the activation function controls how we'll pass that information on to the next layer.

An ideal activation function is both nonlinear and differentiable. The nonlinear behavior of an activation function allows our neural network to learn nonlinear relationships in the data. Differentiability is important because it allows us to backpropagate the model's error when training to optimize the weights.

Note: I'll continue to update this page as I get more practical experience with the activation functions.

Perceptron

While this is the original activation first developed when neural networks were invented, it is no longer used in neural network architectures because it's incompatible with backpropagation. Backpropagation allows us to find the optimal weights for our model using a version of gradient descent; unfortunately, the derivative of a perceptron activation function cannot be used to update the weights (since it is 0).

Function:

f( x )={ 0 for x<0 1 for x≥0 }

Derivative:

f ′ ( x )={ 0 for x≠0 ? for x=0 }

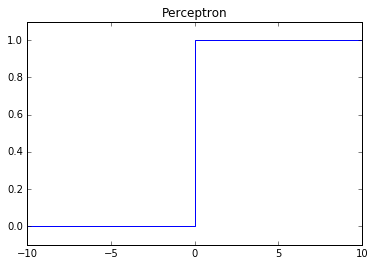
Problems: not compatible gradient descent via backpropagation.

Sigmoid (logistic)

The sigmoid function is commonly used when teaching neural networks, however, it has fallen out of practice to use this activation function in real-world neural networks due to a problem known as the vanishing gradient.

Recall that we included the derivative of the activation function in calculating the "error" term for each layer in the backpropagation algorithm. The maximum value of the derivative for the sigmoid function is 0.25, thus, and you progress backwards each layer in backpropagation you're reducing the size of your "error" by at least 75% at each layer. This ends up limiting our ability to change the weights in layers close to the input layer for deep networks because so many of terms multiplied together in the derivative chain are less than or equal to 0.25.

Function: $$f\left( x \right) = \frac{1}{{1 + {e^{ - x}}}}$$
Derivative: $$f'\left( x \right) = f\left( x \right)\left( {1 - f\left( x \right)} \right)$$

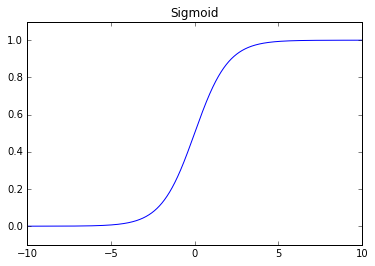
Problems: vanishing gradient at edges, output isn't zero centered.

Hyperbolic Tangent

Function: $$f\left( x \right) = \tanh \left( x \right) = \frac{{{e^x} - {e^{-x}}}}{{{e^x} + {e^{-x}}}}$$
Derivative: $$f'\left( x \right) = 1 - f{\left( x \right)^2}$$

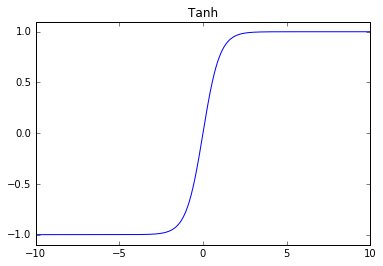
Problems: vanishing gradient at edges.

Inverse Tangent

Function: $$f\left( x \right) = {\tan ^{ - 1}}\left( x \right)$$
Derivative: $$f'\left( x \right) = \frac{1}{{{x^2} + 1}}$$

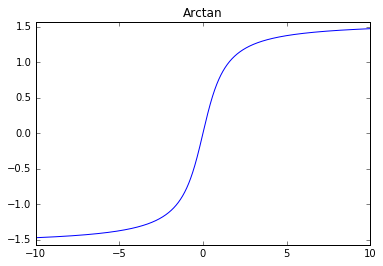
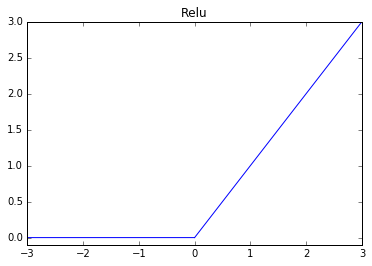
ReLU (rectified linear unit)

This is one of the most popularly used activation functions of 2017. Due to its popularity, a number of variants have been proposed that provide an incremental benefit over standard ReLUs.

Function:

f( x )={ 0 for x<0 x for x≥0 } or (another way to write the ReLU function is...) f( x )=max( x,0 )

Derivative:

f ′ ( x )={ 0 for x<0 1 for x≥0 }

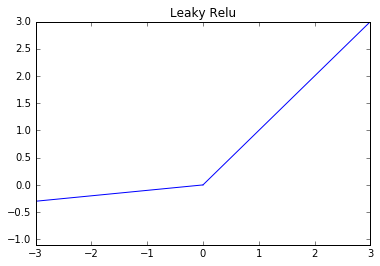
Leaky ReLU

Function:

f( x )={ 0.1x for x<0 x for x≥0 }

Derivative:

f ′ ( x )={ 0.1 for x<0 1 for x≥0 }

SeLU (Scaled-exponential linear units)

The SeLU activation function was proposed as a method to create self-normalizing networks.

Function:

f( α,x )=λ{ α( e x −1 ) for x<0 x for x≥0 }

Derivative:

f ′ ( α,x )=λ{ f( α,x )+α for x<0 1 for x≥0 }

Maxout

Function: $$f\left( {\vec x} \right) = \mathop {\max }\limits_i {x_i}$$
Derivative:

∂f ∂ x j ={ 1 for j= argmax i x i 0 for j≠ argmax i x i }

The following activation functions should only be used on the output layer.

Identity

Function: $$f\left( x \right) = x$$
Derivative: $$f'\left( x \right) = 1$$

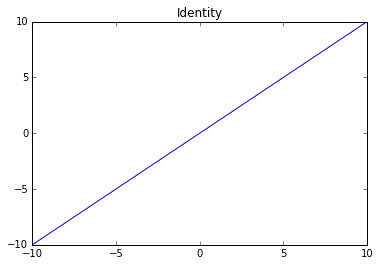
Use: regression.

Softmax

The softmax function is commonly used as the output activation function for multi-class classification because it scales the preceding inputs from a range between 0 and 1 and normalizes the output layer so that the sum of all output neurons is equal to one. As a result, we can consider the softmax function as a categorical probability distribution. This allows you to communicate a degree of confidence in your class predictions.

Note: we use the exponential function to ensure all values in the summation are positive.

Function: $${f_i}\left( {\vec x} \right) = \frac{{{e^{{x_i}}}}}{{\sum\nolimits_{j = 1}^J {{e^{{x_j}}}} }} {\rm{\hspace{2mm} for \hspace{2mm} i = 1,..,J}}$$
Derivative: $$\frac{{\partial {f_i}\left( {\vec x} \right)}}{{\partial {x_j}}} = {f_i}\left( {\vec x} \right)\left( {{\delta_{ij}} - {f_i}\left( {\vec x} \right)} \right)$$

Use: classification.

Further Reading